라그랑주 승수법

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 이론적 배경
4. 다양한 응용
5. 현대적 공식화 (미분다양체)
6. 라그랑주 승수의 해석
7. 한계 및 주의점
8. 예제
참조

1. 개요

라그랑주 승수법은 제약 조건 하에서 함수의 극값을 찾는 최적화 문제 해결에 사용되는 방법이다. 함수 f(x)에 대한 제약 조건 g(x) = 0이 주어질 때, 라그랑주 승수법은 새로운 변수 λ(라그랑주 승수)를 도입하여 라그랑지안 함수 F(x, λ) = f(x) + λ ⋅ g(x)를 정의하고, 이 함수의 정류점을 찾아 원래 문제의 해를 구한다. 이 방법은 경제학, 물리학, 공학, 정보 이론, 인공지능 등 다양한 분야에서 활용되며, 제약 조건의 완화에 따른 목적 함수의 변화율을 나타내는 라그랑주 승수의 해석이 중요하다. 그러나 라그랑주 승수법은 극값의 필요 조건만을 제공하며, 안장점을 극값으로 오인할 수 있다는 한계가 있어, 해의 타당성을 검증하기 위한 추가적인 분석이 필요하다.

더 읽어볼만한 페이지

수학적 최적화 - 제약된 최적화
제약된 최적화는 제약 조건을 만족하는 해 중에서 목적 함수를 최적화하는 해를 찾는 문제로, 자원 할당, 스케줄링 등에 활용되며, 다양한 제약 조건과 해법을 통해 해결될 수 있습니다.
수학적 최적화 - 모서리해
모서리 해는 경제학에서 소비자가 예산 제약 하에 효용을 극대화할 때, 두 상품 중 하나만 소비하는 경우를 의미하며, 이는 소비자의 극단적인 선택이나 완전 대체재 관계에서 가격이 낮은 상품만 구매하는 경우 등에 나타나는 현상입니다.

라그랑주 승수법

2. 정의

연속미분가능한 함수 $f\colon\mathbb R^D\to\mathbb R$ 와 $\mathbf g\colon\mathbb R^D\to\mathbb R^C$ 에 대해, $\mathbf g(\mathbf x)=0$ 이라는 제약 조건 하에서 $f(\mathbf x)$ 의 극값을 찾는 문제를 생각해 보자. 라그랑주 승수법은 이 문제를 다음과 같이 변환한다. 새로운 함수 $F(\mathbf x,\mathbf y)=f(\mathbf x)+\mathbf y\cdot\mathbf g(\mathbf x)$ 를 정의한다. 여기서 $\mathbf y\in\mathbb R^C$ 는 라그랑주 승수라고 불리는 새로운 변수이다. $F$ 의 정류점은 원래 문제의 제약 조건 하에서의 극값과 일치한다. 즉, $F$ 를 $\mathbf x$ 와 $\mathbf y$ 에 대해 편미분하여 0이 되는 지점을 찾으면, 그 지점이 바로 제약 조건 하에서의 $f$ 의 극값이 된다.^[2]

일반적인 경우, 라그랑지안은 다음과 같이 정의된다.^[2]

: $\mathcal{L}(x, \lambda) \equiv f(x) + \langle \lambda, g(x)\rangle$

함수 $f, g$ 에 대해; 표기 $\langle \cdot, \cdot \rangle$ 는 내적을 나타낸다. 값 $\lambda$ 는 라그랑주 승수라고 한다.

내적이 점곱으로 정의되는 간단한 경우, 라그랑지안은 다음과 같다.^[2]

: $\mathcal{L}(x, \lambda) \equiv f(x) + \lambda\cdot g(x)$

이 방법은 $g(x) = 0$ 의 등식 제약 조건 하에서 함수 $f$ 의 최댓값 또는 최솟값을 찾기 위해, $x$ 및 라그랑주 승수 $\lambda$ 의 함수로 간주되는 $\mathcal{L}$ 의 정상점을 찾는 것으로 요약할 수 있다. 즉, $\lambda$ 에 대한 편미분을 포함하여 모든 편미분이 0이어야 한다.^[3]

3. 이론적 배경

라그랑주 승수법의 핵심은 제약 조건 $g(x) = 0$을 만족하는 곡선(또는 곡면) 위에서 함수 $f(x)$의 기울기 벡터와 제약 조건 함수의 기울기 벡터가 평행해야 한다는 것이다. 이는 기하학적으로 $f(x)$의 등고선(또는 등위면)과 $g(x) = 0$이라는 제약 조건 곡선(또는 곡면)이 접하는 지점에서 극값이 발생한다는 것을 의미한다. 라그랑주 승수 $\lambda$는 두 기울기 벡터의 크기 차이를 보정하는 역할을 한다.^[2]

연속미분가능함수 $f\colon\mathbb R^D\to\mathbb R$와 $\mathbf g\colon\mathbb R^D\to\mathbb R^C$를 생각해보자. $\mathbf g(\mathbf x)=0$인 제약 아래 $f(\mathbf x)$를 최적화하는 문제는 라그랑주 승수법을 써서 다음과 같이 풀 수 있다. 함수 $F\colon\mathbb R^{D+C}\to\mathbb R$를 다음과 같이 정의한다.

: $F(\mathbf x,\mathbf y)=f(\mathbf x)+\mathbf y\cdot\mathbf g(\mathbf x)$

$F$의 정류점은 오일러-라그랑주 방정식을 통해 찾을 수 있다.

만약 $(\mathbf x,\mathbf y)\in\mathbb R^{D+C}$가 $F$의 정류점이면, $\mathbf x$는 $\mathbf g=0$으로 제약한 $f$의 정류점이다.
만약 $\mathbf x\in\mathbb R^D$가 $\mathbf g=0$으로 제약한 $f$의 정류점이면, $(\mathbf x,\mathbf y)$가 $F$의 정류점인 $\mathbf y\in\mathbb R^C$가 존재한다.

여기서 보조변수 $\mathbf y\in\mathbb R^C$를 라그랑주 승수(Lagrange multiplier^영어)라고 한다.

최적화 이론에서는 극값을 찾는데, 극점은 정류점의 부분집합이므로 정류점을 모두 찾아 극점인지 확인하면 된다.

일반적인 경우, 라그랑지안은 다음과 같이 정의된다.^[2]

:

\mathcal{L}(x, \lambda) \equiv f(x) + \langle \lambda, g(x)\rangle

함수 $f, g$에 대해; 표기 $\langle \cdot, \cdot \rangle$는 내적을 나타낸다. 값 $\lambda$는 라그랑주 승수라고 한다.

내적이 점곱으로 정의되는 간단한 경우, 라그랑지안은 다음과 같다.

:

\mathcal{L}(x, \lambda) \equiv f(x) + \lambda\cdot g(x)

$g(x) = 0$의 등식 제약 조건 하에서 함수 $f$의 최댓값 또는 최솟값을 찾기 위해, $x$ 및 라그랑주 승수 $\lambda$의 함수로 간주되는 $\mathcal{L}$의 정상점을 찾는다. 즉, $\lambda$에 대한 편미분을 포함하여 모든 편미분이 0이어야 한다.^[3]

:

\frac{ \partial \mathcal{L} }{\partial x} = 0

및

\frac{ \partial \mathcal{L} }{\partial \lambda} = 0\ ;

또는 다음과 같다.

:

\frac{ \partial f(x) }{\partial x} + \lambda\cdot \frac{ \partial g(x) }{\partial x} = 0

및

g(x) = 0 ~.

원래 제약 최적화에 해당하는 해는 항상 라그랑지안 함수의 안장점이며,^[4]^[5] 이는 보더 헤세 행렬의 정부호성으로부터 정상점 중에서 식별될 수 있다.^[6]

라그랑주 승수 방법은 어려운 제약 최적화 문제를 해결하는 데 널리 사용된다. 또한, 라그랑주 승수 방법은 카루쉬-쿤-터커 조건에 의해 일반화된다.

라그랑주 승수 정리는 다음과 같다.^[7]

$f: \mathbb{R}^n \to \mathbb{R}$을 목적 함수, $g: \mathbb{R}^n \to \mathbb{R}^c$를 제약 조건 함수라고 하자. 둘 다 $C^1$에 속한다고 하자(즉, 연속적인 1차 미분을 가진다). $x_\star$을 다음 최적화 문제의 최적해라고 하고, $\Bigl[ \operatorname{D}g(x_\star) \Bigr]_{j,k} = \frac{\ \partial g_j\ }{\partial x_k}$인 편미분 행렬에 대해 $\operatorname{rank} (\operatorname{D}g(x_\star)) = c \le n$이라고 하자.

\begin{align}& \text{최대화 } f(x) \\& \text{제약 조건: } g(x) = 0\end{align}

그러면 고유한 라그랑주 승수 $\lambda_\star \in \mathbb{R}^c$가 존재하여 $\operatorname{D}f(x_\star) = \lambda_\star^{\mathsf{T}}\operatorname{D}g(x_\star)$이 된다.

라그랑주 승수 정리는 등식 제약 조건 하에서 평가된 함수의 모든 지역 최대점(또는 최소점)에서, 제약 조건이 적용되는 경우, 함수의 기울기(그 지점에서)가 라그랑주 승수를 계수로 하여 제약 조건의 기울기(그 지점에서)의 선형 결합으로 표현될 수 있다고 말한다.^[8] 이는 제약 조건의 모든 기울기에 수직인 모든 방향이 함수의 기울기에도 수직이라고 말하는 것과 같다. 또는, 함수의 방향 미분이 모든 실행 가능한 방향에서 0이라고 말하는 것과 같다.

라그랑주 승수법은 여러 개의 제약 조건이 있는 문제를 해결하도록 확장될 수 있다. 단일 점에서 교차하는 두 개의 선형 제약 조건이 있는 포물면을 고려해 보자. 유일한 가능한 해인 이 점은 분명히 제약된 극값이다. 그러나 $f$의 레벨 집합은 교차점에서 어느 제약 조건의 기울기에도 평행하지 않다(위 그림 참조). 대신 두 제약 조건의 기울기의 선형 결합이다.

구체적으로, $M$개의 제약 조건이 있고, $g_i(\mathbf{x}) = 0, i=1, \dots, M$를 만족하는 점 집합을 따라 이동한다고 가정해 보자. 주어진 제약 조건 함수 $g_i$의 등고선 상의 모든 점 $\mathbf{x}$는 허용 가능한 방향의 공간을 갖는다. 즉, $\nabla g_i(\mathbf{x})$에 수직인 벡터의 공간이다. 모든 제약 조건에 의해 허용되는 방향 집합은 모든 제약 조건의 기울기에 수직인 방향의 공간이다. 이 허용 가능한 이동의 공간을 $A$로 표시하고 제약 조건의 기울기의 범위를 $S$로 표시한다. 그러면 $A = S^{\perp}$가 된다. 즉, $S$의 모든 요소에 수직인 벡터의 공간이다.

여전히 $f$가 이동할 때 변하지 않는 점을 찾는 데 관심이 있다. 따라서 $\mathbf{x}$에서 벗어나는 임의의 허용 가능한 이동 방향이 $\nabla f(\mathbf{x})$에 수직이 되도록 하는 $\mathbf{x}$를 찾는다. 즉, $\nabla f(\mathbf{x}) \in A^{\perp} = S$이다. 따라서 다음을 만족하는 스칼라 $\lambda_1, \lambda_2, \dots, \lambda_M$이 존재한다.

:

\nabla f(\mathbf{x}) = \sum_{k=1}^M  \lambda_k \, \nabla g_k (\mathbf{x})  \quad \iff \quad \nabla f(\mathbf{x}) - \sum_{k=1}^M {\lambda_k \nabla g_k (\mathbf{x})} = 0 ~.

이 스칼라가 바로 라그랑주 승수이다. 이제 제약 조건마다 하나씩, $M$개의 승수를 갖게 된다.

이전과 마찬가지로, 보조 함수를 도입한다.

:

\mathcal{L}\left( x_1,\ldots , x_n, \lambda_1, \ldots, \lambda _M \right) = f\left( x_1, \ldots, x_n \right) - \sum\limits_{k=1}^M {\lambda_k g_k\left( x_1, \ldots , x_n \right)}\

그리고 다음을 푼다.

:

\nabla_{x_1, \ldots , x_n, \lambda_1, \ldots, \lambda _M} \mathcal{L}(x_1, \ldots , x_n, \lambda_1, \ldots, \lambda _M)=0 \iff\begin{cases}\nabla f(\mathbf{x}) - \sum_{k=1}^M {\lambda_k \, \nabla g_k (\mathbf{x})} = 0\\g_1(\mathbf{x}) = \cdots = g_M(\mathbf{x}) = 0\end{cases}

이는 $n+M$개의 미지수에 대한 $n+M$개의 방정식을 푸는 것과 같다.

여러 제약 조건이 있는 경우 제약 조건 자격 가정은 관련 지점에서의 제약 조건 기울기가 선형 독립적이라는 것이다.

제약 조건 $g(x, y) = 0$ 하에서 $f(x, y)$가 최대값을 갖는 점 $(a, b)$를 구하는 문제, 즉

:maximize $f(x,y)$,

:subject to $g(x,y) = 0$

라는 문제를 생각한다. 라그랑주 승수를 $\lambda$라고 하고,

:

F(x,y,\lambda) = f(x,y) - \lambda g(x,y)

라고 놓는다. 점 $(a, b)$에서 $\frac{\partial g}{\partial x}$ 와 $\frac{\partial g}{\partial y}$ 중 적어도 하나가 0이 아니라면, $\alpha$가 존재하여 점 $(a, b, \alpha)$에서

:

\frac{\partial F}{\partial x} = \frac{\partial F}{\partial y} = \frac{\partial F}{\partial \lambda} = 0

이 성립한다.^[26]

$n$차원 공간의 점 $\boldsymbol{x} = (x_1, \dots, x_n)$의 어떤 영역 $R$을 정의역으로 하는 피평가 함수 $z = f(\boldsymbol{x})$가, 같은 영역을 정의역으로 하는 $m$차원 벡터 값 함수

:

\boldsymbol{G}(\boldsymbol{x}) = \begin{pmatrix}g_1(x_1,\dots,x_n) \\\vdots \\ g_m(x_1,\dots,x_n)\end{pmatrix} = \boldsymbol{0}\qquad (1)

아래에서, $R$ 내의 점 $\boldsymbol{x}$에서 극값을 가지기 위한 필요 조건은, 그 점에서의 $f$의 기울기(그래디언트) 벡터

:

\nabla f = {}^t\begin{pmatrix}\dfrac{\partial f}{\partial x_1},\dots,\dfrac{\partial f}{\partial x_n}\end{pmatrix}

가, 그 점에서, $m$개의 $g_i$ 각각의 기울기 벡터가 만드는 $m$차원 선형 부분 공간에 포함되는 것, 즉, 스칼라의 조합 $\boldsymbol{\lambda} = (\lambda_1, \dots, \lambda_m)$을 사용하여,

:

\nabla f = \sum_{i=1}^m \lambda_i \nabla g_i \qquad (2)

가 성립하는 것이다. 이항하여 $\nabla$를 취하면,

:

f(\boldsymbol{x}) - \sum_{i=1}^m \lambda_i g_i(\boldsymbol{x})

가 정류점을 가지는 것이다. 단, $\{\nabla g_1, \dots, \nabla g_m\}$은 선형 독립이어야 한다. 식(1)의 $m$개와 식(2)의 $n$개의 식을 연립하여, $\boldsymbol{x}$와 $\boldsymbol{\lambda}$의 $(n + m)$개의 미지수에 대해 풀면, $f$의 극값을 제공하는 후보점을 얻을 수 있다.^[27]

간단하게 2차원의 경우를 생각하면, $g(x, y) = c$ (여기서 $c$는 주어진 상수이다)라는 조건 하에서 함수 $f(x, y)$를 최대화하는 경우를 생각해 보자. $f$의 값을 높이로 하는 그래프를 생각하면, 높이가 $d$인 $f$의 등고선은 $f(x, y) = d$로 주어진다. 여기서 임의의 곡선을 따라 이동하는 점을 생각해 보면, 이 점이 등고선을 가로지를 경우 반드시 $f(x, y)$는 증가하거나 감소하지만, 이 점이 등고선을 따라 이동하는 경우에는 $f(x, y)$는 변하지 않는다는 것을 알 수 있다. 이 조건과 일반적인 극값 조건을 함께 고려하면, 곡선상에서 $f(x, y)$가 최대값을 가지는 점에서는 $f$의 등고선의 접선과 곡선의 접선이 평행하거나, $f$의 기울기가 0이 된다는 것을 알 수 있다. 여기서 $g(x, y) = c$의 접선은 $g$의 기울기 벡터 $\nabla_{x,y} g$와 직교하며, $f$의 등고선 $f(x, y) = d$의 접선은 $f$의 기울기 벡터 $\nabla_{x,y} f$와 직교한다는 점을 감안하면, 앞서 언급한 조건은 다음과 같이 쓸 수 있다.

:

\nabla_{x,y} f = \lambda \nabla_{x,y} g

여기서

:

\nabla_{x,y} f= \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right), \qquad \nabla_{x,y} g= \left( \frac{\partial g}{\partial x}, \frac{\partial g}{\partial y} \right)

이다. 상수 $\lambda$는 $f$의 기울기 벡터와 $g$의 기울기 벡터가 평행하지만 길이가 일반적으로 다르기 때문에 필요하다. $\lambda = 0$인 경우, $f(x, y)$의 기울기가 0이 되는 조건이 된다.

앞서 언급한 식을 변형하면

:

\nabla_{x,y} (f-\lambda g)=0

이 되므로, $f - \lambda g$의 극값을 구하면 된다.

다음과 같은 두 가지 유사한 문제를 생각해 보자.
문제 A$x\in \mathbb{R}^n$이 제약 조건 $g(x)=0$을 만족하는 조건 하에서, $f(x)$를 극대화하는 점을 구하라.
문제 B$\lambda$를 상수라고 하고, $x\in \mathbb{R}^n$이 $h(x)=f(x)-\lambda g(x)$를 극대화하는 점을 구하라.

문제 A는 제약 조건이 존재하기 때문에 "각 변수로 편미분하여, 편미분 계수가 0이 되는 점을 구하는" 해법을 사용할 수 없는 반면, 문제 B에는 제약 조건이 없으므로, "각 변수로 편미분하여, 편미분 계수가 0이 되는 점을 구하는" 해법을 사용할 수 있다. 라그랑주 미정 승수법은 문제 A와 문제 B가 실질적으로 동일하다는 것을 말한다.
문제 B → 문제 A$X\in \mathbb{R}^n$을 어떤 $\lambda$에 대한 문제 B의 극대점이라고 하고, 또한 $X$가 $g(X)=0$을 만족하면, $X$는 문제 A의 해이다.

왜냐하면, $X$의 근방에서 $g(x)=0$이 되는 점 $x$를 생각하면,

:

f(x)=f(x)-\lambda g(x)\le f(X)-\lambda g(X)=f(X)

가 되므로, $X$는 문제 A의 극대점이기도 하다.
문제 A → 문제 B$X\in \mathbb{R}^n$을 문제 A의 극대점으로 한다.

$c(t) \in \mathbb{R}^n$, $t \in (-1,1)$을, $g( c(t) )=0$을 만족하고 $X$를 통과하는 곡선으로 하고, $c(0)=X$로 한다.

$F(t)=f( c(t) )$를 $t$의 함수로 생각한다.

:

\frac{dF}{dt}=\sum_{i=1}^n\frac{\partial f}{\partial x_i} \frac{d c_i}{dt}=\nabla f \cdot c'(t)

단, $\nabla f= (\partial f/\partial x_1,\cdots , \partial f/\partial x_n)$, $c'(t)= (d c_1/dt,\cdots ,dc_n/dt)$, "$\cdot$"는 벡터의 내적이다.

한편, $g( c(t) )=0$의 양변을 $t$로 미분하면,

:

\nabla g \cdot c'(t)=0

임을 알 수 있다.

$g( c(t) )=0$을 만족하고 $X$를 통과하는 어떠한 곡선이라도, $t=0$은, $c(0)=X$이므로 $F(t)=f( c(t) )$의 극대점이며, $\frac{dF}{dt}(0)=\nabla f (X)\cdot c'(0)=0$임을 알 수 있다. 단, $c'(0)$는 곡선의 $X$에서의 접선 벡터이다.

:$X$가 문제 A의 극대점이면,

:$\nabla g(X) \cdot v=0$을 만족하는 어떠한 $v\in \mathbb{R}^n$에 대해서도,

:$\nabla f(X) \cdot v=0$이다.

$\nabla g(X)\ne 0$이라고 가정하고, $\nabla f(X)$를, $\nabla g(X)$에 평행한 성분 $a$와, $\nabla g(X)$에 수직인 성분 $b$로 분해한다. ($\nabla g(X)$ 방향의 단위 벡터를 $e$라고 하면, $a=(\nabla f(X)\cdot e)e$, $b=\nabla f(X)-a$이다.) $\nabla f(X)=a+b$

$\nabla g(X) \cdot b=0$이므로 $v=b$로 대입하면,

$0=\nabla f(X) \cdot b=a\cdot b+b\cdot b=b\cdot b$, 따라서 $b=0$

이 때문에, $\nabla f(X)$와 $\nabla g(X)$는 평행하다.

:

\nabla f(X)=\lambda \nabla g(X)

, (단, $\nabla g(X)\ne 0$을 가정했다.)

이 $\lambda$에 대해 문제 B를 생각하면, $\nabla f(X)-\lambda \nabla g(X)=0$이므로,

:

\frac{\partial h}{\partial x_i}(X)=\frac{\partial f}{\partial x_i}(X)-\lambda \frac{\partial g}{\partial x_i}(X)=0

가 되어, 모든 편미분 계수가 0이 되므로, $X$는 문제 B의 극대점이기도 하다.

4. 다양한 응용

라그랑주 승수법은 다양한 분야에서 활용된다.

미분 가능 다양체 $M$ 에서 국소 최댓값과 최솟값을 찾는 문제는 제약 조건 하에서 국소 최댓값과 최솟값을 찾는 문제의 일반화된 경우이다.^[14] 이때, $M$ 은 유클리드 공간이나 리만 다양체일 필요는 없으며, 기울기 $\nabla$ 는 외미분 $\operatorname{d}$ 로 대체될 수 있다.

이산 확률 분포에서 정보 엔트로피가 최대가 되는 확률 분포를 찾는 문제를 생각해보자. 이는 가장 구조화되지 않은 확률 분포를 찾는 것과 같으며, 섀넌 엔트로피 방정식을 최대화하는 문제이다. 확률 분포의 합은 1이라는 제약 조건 하에 라그랑주 승수법을 사용하면, 모든 사건이 동일한 확률을 가지는 균등 분포가 엔트로피가 최대인 분포임을 알 수 있다.

4. 1. 경제학

많은 수리 경제학 모델, 예를 들어 일반 균형 모형에서 소비자의 행동은 효용 극대화로, 기업의 행동은 이윤 극대화로 구현되며, 두 주체 모두 예산 제약 및 생산 제약과 같은 제약 조건의 적용을 받는다. 최적의 해를 결정하는 일반적인 방법은 라그랑주 승수를 사용하여 제약 조건을 적용하여 어떤 함수를 극대화함으로써 달성된다.

제약 조건을 예산 제약선, 함수를 효용 함수, 극값을 최적 소비점으로 바꿔 미시 경제학에서 최적 소비점을 구하는 데 이용된다.^[29] 이때 라그랑주 승수는 화폐의 한계 효용으로 해석할 수 있다.

4. 2. 물리학

물리학에서 라그랑주 승수는 단순한 계산상의 편의가 아니라 어떤 물리량을 나타내는 경우가 많다.

유체역학에서 비압축성 유동의 나비에-스토크스 방정식을 풀 때, 압력은 속도 벡터장이 연속 방정식이라는 구속 조건을 만족시키기 위한 미정 승수로 구해진다.

통계역학에서는 통계적 앙상블이 특정 에너지 상태를 가질 확률을 유도하기 위해 미정 승수법이 사용된다.

작용 적분이 S[q]^영어로 주어지는 물리계에 n개의 구속 조건 φa(q, t) = 0, (a = 1, ..., n)^영어이 주어졌을 때, 이 계의 운동 방정식은 λa^영어를 미정 승수로 하는 조건부 변분

:

\frac{\delta S}{\delta q} + \sum_{a=1}^n \lambda_a \frac{\partial \phi^a}{\partial q} = 0

에 의해 표현된다.^[30] 여기서 δS/δq^영어는 범함수 미분이다. 라그랑주 운동 방정식으로 나타내면, 라그랑지안을

:

L(q,\dot{q},t) + \sum_{a=1}^n \lambda_a \phi^a(q,t)

로 대체함으로써 구속을 고려한 운동 방정식을 얻을 수 있다.

4. 3. 공학

라그랑주 승수법은 최적 제어 이론에서 코상태 변수로 해석되며, 폰트랴긴의 최대 원리에서 해밀토니안의 최소화로 재구성된다.

라그랑주 승수법 기반 방법은 전력 시스템 분야에서 활용되며, 분산 에너지 자원(DER) 배치 및 부하 차단 등에도 적용된다.^[23]

4. 4. 정보 이론

이산 확률 분포 {p₁, p₂, ..., p_n}에서 정보 엔트로피가 최대가 되는 확률 분포를 찾는 경우를 생각해 보자. 이는 {p₁, p₂, …, p_n}에서 가장 구조화되지 않은 확률 분포를 찾는 것과 같다. 즉, 섀넌 엔트로피 방정식을 최대화하는 것이다.

:

f(p_1,p_2,\dots,p_n) = -\sum_{k=1}^n p_k\log_2 p_k

이 확률들의 합은 1이 되어야 하므로, 제약 조건은 다음과 같다.

:

g(p_1,p_2,\dots,p_n)=\sum_{k=1}^n p_k -1

라그랑주 승수법을 사용하여 엔트로피가 최대가 되는 점을 찾을 수 있다. 모든 i (1부터 n까지)에 대해 다음 조건이 필요하다.

:

\frac{\partial}{\partial p_i}(f+\lambda g)=0.

이를 계산하면 다음의 n개 방정식을 얻는다.

:

-\left(\frac{1}{\ln 2}+\log_2 p_i \right) + \lambda = 0.

이것은 모든 p_i가 같다는 것을 의미한다(λ에만 의존하기 때문).

제약 조건

\sum_j p_j =1

을 사용하면,

:

p_i = \frac{1}{n}

임을 알 수 있다. 즉, 모든 사건이 동일한 확률을 가지는 균등 분포가 엔트로피가 최대인 분포이다. 이는 다른 어떤 확률 분포보다 확률 변수가 실제로 관측되었을 때 얻을 수 있는 정보량의 기댓값이 크다는 것을 의미한다.

4. 5. 인공지능

라그랑주 승수법은 제약 마르코프 결정 과정에 적용되며,^[24] 이는 안전 강화 학습에서 자연스럽게 기울기 기반의 프라이멀-듀얼 알고리즘을 생성한다.^[25]

5. 현대적 공식화 (미분다양체)

라그랑주 승수법은 미분다양체를 이용하여 일반화할 수 있다.

'''m'''차원 매끄러운 다양체 $M$ 과 매끄러운 함수 $f: M \to \mathbb{R}$ 가 주어졌을 때, $g(x) = 0$ 으로 정의되는 부분다양체 $N$ 에서 $f$ 의 정류점 $x$ 를 찾는 문제를 생각해보자. 여기서 $g: M \to \mathbb{R}$ 는 0이 정칙값인 매끄러운 함수이다.

$\operatorname{d}f$ 와 $\operatorname{d}g$ 를 각각 $f$ 와 $g$ 의 외미분이라고 하면, $x \in N$ 에서 $f|_N$ 의 정류성은 $\operatorname{d}(f|_N)_x=0$ 을 의미한다. 이는 $\ker(\operatorname{d}f_x)$ 가 $T_x N = \ker(\operatorname{d}g_x)$ 를 포함한다는 뜻이다. 즉, $\operatorname{d}f_x$ 와 $\operatorname{d}g_x$ 는 비례하는 1-형식이다. 이를 위해 다음의 방정식이 성립해야 한다.

: $\operatorname{d}f_x \wedge \operatorname{d}g_x = 0 \in \Lambda^2(T^{\ast}_x M)$

여기서 $\wedge$ 는 외대수의 외곱을 나타낸다. 정류점 $x$ 는 위 방정식과 제약 조건 $g(x) = 0$ 을 만족하는 해이다.

이 공식에서는 라그랑주 승수, 즉 $\operatorname{d}f_x = \lambda \cdot \operatorname{d}g_x$ 를 만족하는 숫자 $\lambda$ 를 명시적으로 찾을 필요가 없다.
다중 제약 조건단일 제약 조건 대신, $p > 1$ 개의 함수 $g_i: M \to \R$ 를 가진 매끄러운 함수 $G:M\to \R^p$ 를 고려하고, $0\in\R^p$ 가 정칙값이라고 하자. $N$ 을 $G(x)=0$ 으로 정의된 $M$ 의 부분다양체라고 하면,

$x$ 가 $f|_{N}$ 의 정지점인 것은 $\ \ker( \operatorname{d}f_x )\$ 가 $\ \ker( \operatorname{d}G_x )$ 를 포함하는 경우뿐이다. $\ L_x = \operatorname{d}f_x\$ 와 $\ K_x = \operatorname{d}G_x\$ 라고 하면, $\ \ker(K_x)$ 는 $\ \ker(L_x)\$ 에 속하며, $L_x \in T^{\ast}_x M$ 이 $\ K^{\ast}_x: \R^{p\ast}\to T^{\ast}_x M ~$ 의 이미지에 속하는 경우에만 해당한다.

$\ \omega_x \in \Lambda^{p}(T^{\ast}_x M)\$ 가 $\ K^{\ast}_x$ 행렬의 열의 외적을 나타내는 경우, $\ f|_{N}\$ 의 $\ x\$ 에서의 정지 조건은 다음과 같다.

: $L_x \wedge \omega_x = 0 \in \Lambda^{p+1} \left (T^{\ast}_x M \right )$

이 경우에도 라그랑주 승수 $\ \lambda_1, \ldots, \lambda_p\$ 를 명시적으로 찾을 필요가 없다.

6. 라그랑주 승수의 해석

라그랑주 승수는 제약 조건 매개변수의 함수로서 최적화되는 양의 변화율을 나타낸다. 즉, 제약 조건이 변화함에 따라 목적 함수가 얼마나 변하는지를 보여주는 값이다.

예를 들어, 라그랑주 역학에서 운동 방정식은 작용의 정지점을 찾아 유도되는데, 작용은 운동 에너지와 위치 에너지의 차이를 시간에 대해 적분한 것이다. 스칼라 퍼텐셜에 의해 입자에 작용하는 힘은, 입자의 제약된 궤적의 변화에 따른 작용의 변화 (위치 에너지의 운동 에너지로의 전이)를 결정하는 라그랑주 승수로 해석될 수 있다.

제어 이론에서는 이를 공동 상태 방정식으로 공식화한다.

포락선 정리에 의해 라그랑주 승수의 최적 값은, 원래 목적 함수의 최적 달성 가능 값에 대한 해당 제약 상수의 한계 효과로 해석된다. 최적 값에서 별표( $\star$ )로 값을 나타내면 다음이 성립한다.

$\frac{\ \operatorname{d} f\left(\ x_{1 \star }(c_1, c_2, \dots),\ x_{2 \star }(c_1, c_2, \dots),\ \dots\ \right)\ }{ \operatorname{d} c_k } = \lambda_{\star k} ~.$

경제학에서 플레이어의 최적 이윤은 제약된 행동 공간을 전제로 계산되며, 여기서 라그랑주 승수는 주어진 제약 조건의 완화(예: 소득 변화)로 인한 목적 함수(이윤)의 최적 값의 변화를 의미한다. 이러한 맥락에서 $\lambda_{\star k}$ 는 제약 조건의 한계 비용이며, 그림자 가격이라고 불린다.^[15]

7. 한계 및 주의점

라그랑주 승수법은 제약 조건 하에서 극값을 찾는 데 유용한 도구이지만, 몇 가지 한계와 주의점이 있다.

라그랑주 승수법으로 찾은 정류점(stationary point)은 반드시 극값(최댓값 또는 최솟값)이 아닐 수 있다. 정류점은 극점일 수도 있지만, 안장점(saddle point)일 수도 있다.^[4]^[17] 즉, 라그랑주 승수법은 극값을 찾기 위한 필요조건을 제공할 뿐, 충분조건은 아니다.

예를 들어, 함수 $f(x) = x^2$ 에 대해 $x^2 = 1$ 이라는 제약 조건 하에서 최솟값을 찾는 문제를 생각해보자. 라그랑주 승수법을 사용하면 다음과 같은 함수를 정의할 수 있다.

: $\mathcal{L}(x, \lambda) = x^2 + \lambda(x^2 - 1)$

이 함수의 임계점은 $x = 1$ 과 $x = -1$ 에서 발생하는데, 이들은 모두 안장점이다.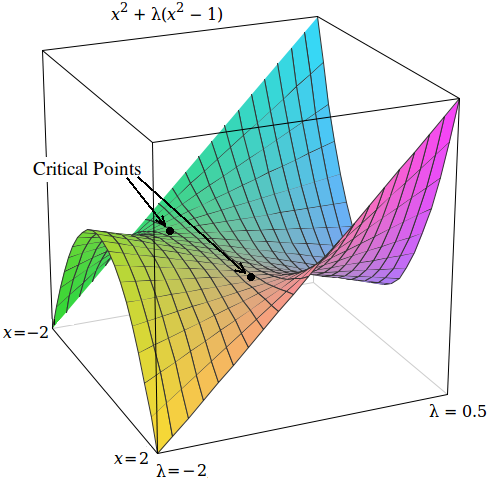

기울기의 크기는 임계점이 지역 최솟값(예제 5)에서 발생하도록 할 수 있다.

따라서 라그랑주 승수법으로 얻은 해가 실제로 극값인지 확인하기 위해 추가적인 분석이 필요할 수 있다. 예를 들어, 헤세 행렬을 이용하여 제약 조건이 있는 극값에 대한 충분 조건을 확인할 수 있다.^[6]^[16]

또한, 언덕 오르기, 경사 하강법 등 많은 수치적 최적화 기법들은 안장점이 아닌 지역 최댓값 또는 최솟값을 찾도록 설계되어 있다. 따라서 라그랑주 승수법을 통해 얻은 해를 이러한 기법에 적용할 때는 주의해야 한다. 필요하다면, 라그랑지안의 기울기의 제곱을 극대화하는 등 공식을 수정하거나, 극값을 찾지 않고 정지점을 찾는 최적화 기법(예: 극값을 찾는 선형 탐색이 없는 뉴턴 방법)을 사용해야 한다.

8. 예제

Lagrange multiplier^영어를 사용하는 예제를 통해 라그랑주 승수법의 적용 과정을 살펴본다.

하나의 제약 조건과 두 개의 선택 변수만 있는 경우를 그림 1을 통해 살펴보자. 다음 최적화 문제를 고려한다.^[9]^[10]^[11]^[12]^[13]

: $\begin{aligned}\underset{x,y}{\text{maximize}} \quad& f(x,y) \\\text{subject to}\quad& g(x,y) = 0.\end{aligned}$

$f$ 와 $g$ 모두 연속적인 1차 편미분을 갖는다고 가정한다. 새로운 변수( $\lambda$ )를 '''라그랑주 승수'''라고 도입하고, '''라그랑주 함수'''를 다음과 같이 정의한다.

: $\mathcal{L}(x,y,\lambda) = f(x,y) + \lambda\cdot g(x,y)$

여기서 $\lambda$ 항은 더하거나 뺄 수 있다. 만약 $f(x_0, y_0)$ 가 원래 제약 문제의 $f(x,y)$ 의 최댓값이고 $\nabla g(x_0,y_0) \ne 0 ,$ 이라면, ( $x_0, y_0, \lambda_0$ )가 라그랑주 함수의 ''정류점''이 되는 $\lambda_0$ 가 존재한다. 그러나 모든 정류점이 원래 문제의 해를 산출하는 것은 아니다.

'''예제 1'''

$\ f(x,y) = x+y\$ 를 제약 조건 $\ x^2 + y^2 = 1 ~.$ 하에서 최대화하는 문제를 생각해보자. 실현 가능 집합은 단위 원이고, 의 등위선은 대각선(기울기 -1)이므로, 최댓값은 $\ \left(\tfrac{1}{\sqrt{2}}, \tfrac{1}{\sqrt{2}}\right)\ ,$ 에서 발생하고 최솟값은 $\ \left(-\tfrac{1}{\sqrt{2}}, -\tfrac{1}{\sqrt{2}}\right) ~.$ 에서 발생함을 그래프로 확인할 수 있다.

라그랑주 승수법을 적용하면, 제약 조건은

: $g(x,y) = x^2 + y^2-1 = 0\ ,$

이므로, 라그랑지 함수는

: $\begin{align}\mathcal{L}(x, y, \lambda) &= f(x,y) + \lambda \cdot g(x,y) \\[4pt]&= x + y + \lambda (x^2 + y^2 - 1)\ ,\end{align}$

가 된다.

이제 기울기를 계산하면

: $\begin{align}\nabla_{x,y,\lambda} \mathcal{L}(x , y, \lambda) &= \left( \frac{\partial \mathcal{L}}{\partial x}, \frac{\partial \mathcal{L}}{\partial y}, \frac{\partial \mathcal{L}}{\partial \lambda} \right ) \\[4pt]&= \left ( 1 + 2 \lambda x, 1 + 2 \lambda y, x^2 + y^2 -1 \right)\end{align}$

이므로,

: $\nabla_{x,y,\lambda} \mathcal{L}(x , y, \lambda)=0 \quad \Leftrightarrow \quad \begin{cases} 1 + 2 \lambda x = 0 \\ 1 + 2 \lambda y = 0 \\ x^2 + y^2 -1 = 0 \end{cases}$

를 얻는다.

마지막 방정식이 원래의 제약 조건이다. 처음 두 방정식으로부터

: $x = y = - \frac{1}{2\lambda}, \qquad \lambda \neq 0 ~.$

을 얻고, 마지막 방정식에 대입하면

: $\frac{1}{4\lambda^2} + \frac{1}{4\lambda^2} - 1 = 0\ ,$

이므로,

: $\lambda = \pm \frac{1}{\sqrt{2\ }}\ ,$

이다. 따라서 $\mathcal{L}$ 의 정류점은

: $\left(\tfrac{\sqrt{2\ }}{2}, \tfrac{\sqrt{2\ }}{2}, -\tfrac{1}{\sqrt{2\ }}\right), \qquad \left(-\tfrac{\sqrt{2\ }}{2}, -\tfrac{\sqrt{2\ }}{2}, \tfrac{1}{\sqrt{2\ }} \right) ~.$

이다.

이 점들에서 목적 함수 의 값을 계산하면

: $f\left(\tfrac{\sqrt{2\ }}{2}, \tfrac{\sqrt{2\ }}{2}\right) = \sqrt{2\ }\ , \qquad f\left(-\tfrac{\sqrt{2\ }}{2}, -\tfrac{\sqrt{2\ }}{2} \right) = -\sqrt{2\ } ~.$

이다.

따라서 제약 조건 하에서의 최댓값은 $\ \sqrt{2\ }\$ 이고, 최솟값은 $-\sqrt{2}$ 이다.

'''예제 2'''

예제 '''1'''의 목적 함수를 $\ f(x,y) = (x + y)^2\$ 로 수정하고, 제약 조건은 $\ g(x,y)=x^2+y^2-1 = 0 ~.$ 으로 동일하게 유지하여 최소화 문제를 살펴보자. 이제 의 등위 집합은 여전히 기울기가 −1인 직선이며, 이러한 등위 집합에 접하는 원의 점은 $\ (\sqrt{2}/2,\sqrt{2}/2)\$ 및 $\ (-\sqrt{2}/2,-\sqrt{2}/2) ~.$ 이다. 이 접점은 $\ f ~.$ 의 최댓값이다.

반면에, 최솟값은 $\ f = 0\$ 에 대한 등위 집합에서 발생하며, $\ (\sqrt{2}/2,-\sqrt{2}/2)\$ 및 $\ (-\sqrt{2}/2, \sqrt{2}/2)\ ,$ 에서 $\ f\$ 의 등위 곡선은 제약 조건에 접하지 않는다. $\ \nabla_{x,y,\lambda}\left(f(x,y)+\lambda\cdot g(x,y) \right)=0\$ 조건은 네 점 모두를 극점으로 정확하게 식별한다. 최솟값은 $\ \lambda =0\$ 에 의해, 최댓값은 $\ \lambda = -2 ~.$ 에 의해 특징지어진다.

'''예제 3'''

이 예는 계산이 더 복잡하지만, 여전히 단일 제약 조건 문제이다.

다음 함수의 최댓값을 구하는 문제를 생각해보자.

: $f(x, y) = x^2 y$

여기서 $\ x\$ 및 $\ y\$ 좌표는 반지름이 $\ \sqrt{3\ } ~.$ 인 원 위에 있다는 제약 조건이 있다. 즉,

: $g(x,y) = x^2 + y^2 - 3 = 0 ~.$

제약 조건이 하나이므로, 라그랑주 승수 $\ \lambda ~.$ 를 사용한다.

제약 조건 $\ g(x,y)\$ 는 반지름이 $\ \sqrt{3\ } ~.$ 인 원에서 0이다. 일반적인 라그랑주 승수법을 적용하면

: $\begin{align}\mathcal{L}(x, y, \lambda) &= f(x,y) + \lambda \cdot g(x, y) \\&= x^2y + \lambda (x^2 + y^2 - 3)\ ,\end{align}$

이므로, 기울기를 계산하면

: $\begin{align}\nabla_{x,y,\lambda} \mathcal{L}(x , y, \lambda) &= \left ( \frac{\partial \mathcal{L}}{\partial x}, \frac{\partial \mathcal{L}}{\partial y}, \frac{\partial \mathcal{L}}{\partial \lambda} \right) \\&= \left ( 2 x y + 2 \lambda x, x^2 + 2 \lambda y, x^2 + y^2 -3 \right) ~.\end{align}$

이다. 따라서

: $\nabla_{x,y,\lambda} \mathcal{L}(x , y, \lambda)=0 \quad \iff \quad \begin{cases}2 x y + 2 \lambda x = 0 \\x^2 + 2 \lambda y = 0 \\x^2 + y^2 - 3 = 0\end{cases} \quad \iff \quad \begin{cases}x (y + \lambda) = 0 & \text{(i)} \\x^2 = -2 \lambda y & \text{(ii)} \\x^2 + y^2 = 3 & \text{(iii)}\end{cases}$

를 얻는다.

(iii)은 원래 제약 조건이다. (i)는 $\ x=0\$ 또는 $\ \lambda=-y ~.$ 을 의미한다. $x=0$ 이면 (iii)에 의해 $\ y = \pm \sqrt{3\ }\$ 이고, (ii)에서 $\ \lambda=0\$ 이다. $\ \lambda=-y\ ,$ 이라면, (ii)에 대입하여 $\ x^2 = 2y^2 ~.$ 을 얻는다. 이를 (iii)에 대입하고 $\ y\$ 에 대해 풀면 $\ y=\pm1 ~.$ 이 된다. 따라서 $\ \mathcal{L}\$ 에는 6개의 임계점이 있다.

: $(\sqrt{2\ },1,-1); \quad (-\sqrt{2\ },1,-1); \quad (\sqrt{2\ },-1,1); \quad (-\sqrt{2\ },-1,1); \quad (0,\sqrt{3\ }, 0); \quad (0,-\sqrt{3\ }, 0) ~.$

이 점들에서 목적 함수를 평가하면

: $f(\pm\sqrt{2\ },1) = 2; \quad f(\pm\sqrt{2\ },-1) = -2; \quad f(0,\pm \sqrt{3\ }) = 0 ~.$

이다.

따라서 목적 함수는 $\ (\pm\sqrt{2\ },1\ )$ 에서 전역 최댓값(제약 조건 하에서)을, $\ (\pm\sqrt{2\ },-1) ~.$ 에서 전역 최솟값을 얻는다. 점 $\ (0,\sqrt{3\ })\$ 은 $\ f\$ 의 지역 최솟값이며, $\ (0,-\sqrt{3\ })\$ 은 $\ f\$ 의 지역 최댓값이다.

'''예제 4'''

구체적인 예를 통해 라그랑주 승수법의 활용을 설명한다.

문제: 제약 조건 하에서 가 최대값을 갖는 점 를 구하라. 즉,

:maximize $f(x,y),$

:subject to $g(x,y) = 0$

라그랑주 승수를 라고 하고,

라고 놓는다. 점 에서 와 중 적어도 하나가 0이 아니라면, 가 존재하여 점 에서

: $\frac{\partial F}{\partial x} = \frac{\partial F}{\partial y} = \frac{\partial F}{\partial \lambda} = 0$

이 성립한다.^[26]

'''예제 5'''

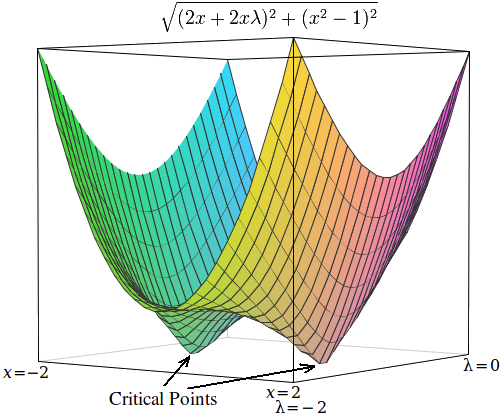
라그랑지안의 임계점은 지역 최대값(또는 최소값)이 아닌 안장점에서 발생한다.^[4]^[17]

$\ f(x) = x^2\ ,$ 를 최소화하는 의 값을 찾는 문제를 생각해보자. 제약 조건은 $\ x^2 = 1 ~.$ 이다.

라그랑주 승수를 사용하면 이 문제를 비제약 최적화 문제로 변환할 수 있다.

: $\mathcal{L}( x, \lambda ) = x^2 + \lambda(x^2-1) ~.$

두 임계점은 및 인 안장점에서 발생한다.

수치 최적화 기법으로 이 문제를 해결하려면 먼저 임계점이 지역 최소값에서 발생하도록 이 문제를 변환해야 한다. 이는 비제약 최적화 문제의 기울기의 크기를 계산하여 수행한다.

먼저, 각 변수에 대한 비제약 문제의 편미분을 계산한다.

: $\begin{align}& \frac{\partial \mathcal{L} }{ \partial x } = 2x + 2x \lambda \\[5pt]& \frac{\partial \mathcal{L} }{ \partial \lambda }=x^2-1 ~.\end{align}$

다음으로, 기울기의 크기를 계산한다. 이는 편미분 제곱의 합의 제곱근이다.

: $\begin{align}h(x,\lambda) & = \sqrt{ (2x+2x\lambda)^2 + (x^2-1)^2\ } \\[4pt]& \approx \sqrt{ \left(\frac{\ \mathcal{L}(x+\varepsilon,\lambda)-\mathcal{L}(x,\lambda)\ }{\varepsilon}\right)^2 + \left(\frac{\ \mathcal{L}(x,\lambda+\varepsilon) - \mathcal{L}(x,\lambda)\ }{\varepsilon}\right)^2\ }~ .\end{align}$

의 임계점은 $\mathcal{L} ~.$ 과 마찬가지로 및 에서 발생한다. 그러나 $\mathcal{L}\,$ 의 임계점과 달리 의 임계점은 지역 최소값에서 발생하므로 수치 최적화 기법을 사용하여 찾을 수 있다.

참조

_[1] 서적 Calculus for Business, Economics, and the Social and Life Sciences
_[2] 서적 Optimization and Stability Theory for Economic Analysis Cambridge University Press
_[3] 서적 Intermediate Calculus Springer
_[4] 서적 Methods of Optimization John Wiley & Sons
_[5] 간행물 Leveling with Lagrange: An alternate view of constrained optimization
_[6] 서적 The Structure of Economics: A Mathematical Analysis Irwin McGraw-Hill
_[7] 서적 Mathematical Methods and Models for Economists https://archive.org/[...] Cambridge University Press
_[8] 서적 Optimization by Vector Space Methods John Wiley & Sons
_[9] 서적 Nonlinear Programming Athena Scientific
_[10] 서적 Lagrange multipliers
_[11] 서적 Optimization Theory for Large Systems Dover
_[12] 서적 Convex analysis and minimization algorithms Springer-Verlag
_[13] 학회자료 Lagrangian relaxation Springer-Verlag 2000-05-15
_[14] 서적 An Introduction to Differential Manifolds https://books.google[...] Springer
_[15] 서적 Optimization in Economic Theory Oxford University Press
_[16] 서적 Fundamental Methods of Mathematical Economics https://archive.org/[...] McGraw-Hill 1984
_[17] 서적 Scientific Computing: An introductory survey https://books.google[...] McGraw-Hill
_[18] 간행물 Modern multiplier rules http://www.maa.org/p[...] 1980
_[19] 서적 Dynamic Optimization: The Calculus of Variations and Optimal Control in Economics and Management https://books.google[...] Elsevier
_[20] 간행물 From constrained optimization to constrained dynamics: extending analogies between economics and mechanics 2019
_[21] 간행물 Lagrange Multiplier Problems in Economics 1984
_[22] 간행물 Applications of a constrained mechanics methodology in economics 2011
_[23] 학회자료 A sensitivity-based approach to adaptive under-frequency load shedding Institute of Electronic and Electrical Engineers
_[24] 서적 Constrained Markov Decision Processes Routledge
_[25] 학회자료 Natural policy gradient primal-dual method for constrained Markov decision processes
_[26] 서적 入門微分積分培風館
_[27] 간행물 学力低下時代の教え方第4回ラグランジの未定係数法一般社団法人日本機械学会 2009-12
_[28] 서적 コンピュータによる流体力学シュプリンガー・フェアラーク東京
_[29] 웹사이트 ラグランジュ未定乗数法でミクロ経済学の効用最大化問題を解く https://kitaguni-eco[...] 2019-11-04
_[30] 서적 現代解析力学入門朝倉書店

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com